Finding Prime Numbers using Sieve of Eratosthenes algorithm

Prime numbers are natural numbers greater than 1 that have no positive divisors other than 1 and themselves, such as 2, 3, 5, and 7. They are widely used in various fields, including cryptography for secure communication, mathematics for number theory, computer science for hash functions and algorithms, error detection in data transmission, and signal processing.

List of primes up to 1000

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997

However, computing prime numbers, especially large ones, is very challenging and computationally intensive. Today, we’ll explore the Sieve of Eratosthenes algorithm, an efficient method for finding prime numbers.

What is the Sieve of Eratosthenes?

The Sieve of Eratosthenes is an efficient algorithm for finding all prime numbers up to a given limit. It works by iteratively marking the multiples of each prime number as composite (not prime), starting from 2. The algorithm is named after Eratosthenes of Cyrene, a Greek mathematician from the 3rd century BCE.

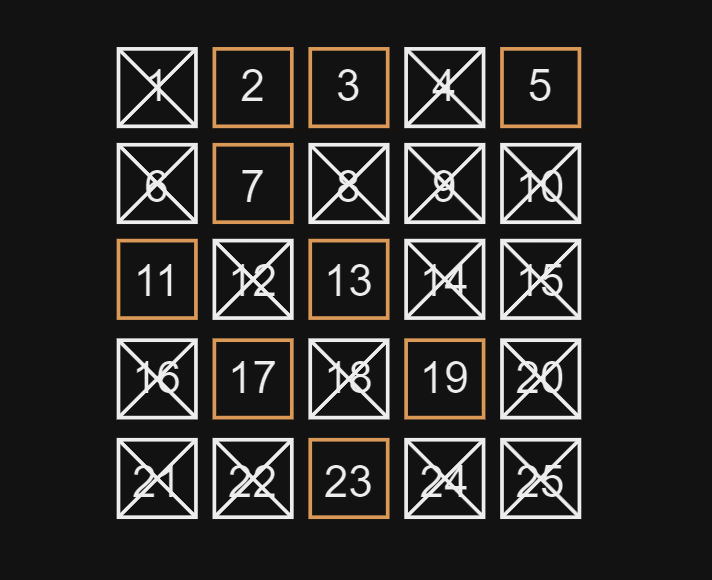
Implementing the Sieve in TypeScript

Here’s the basic implementation of this algorithm in TypeScript. Feel free to experiment with the code in my playground, try different limits, and see how quickly you can generate large sets of prime numbers!

We create a boolean array called table with limit + 1 elements, initially all set to true.
Since 0 and 1 are not primes, we mark the 0th and 1st elements of our table as false.
We iterate from 2 to the square root of the limit, because any composite number larger than √limit must have a factor less than or equal to √limit.
For each prime number found, we mark all its multiples as composite.
Finally, we collect all the numbers that are still marked as prime into an array and return it.

function sieveOfEratosthenes(limit: number): number[] {
	
  const table: boolean[] = Array(limit + 1).fill(true);
  
  table[0] = table[1] = false;

  for (let n = 2; n ** 2 <= limit; n++) {
    for (let k = n ** 2; k <= limit; k += n) {
      table[k] = false;
    }
  }

  const primes: number[] = []

  for (let n = 2; n <= limit; n++) {
    if (table[n]) {
      primes.push(n);
    }
  }

  return primes;
}

Time and Space Complexity

The time complexity of this implementation is O(n log log n), where n is the input limit. This makes it more efficient than naive approaches that check each number individually.

The space complexity is O(n) since we use an array of size n+1 to store the boolean values.

And that’s it. Now you know how to compute primes quickly using this interesting algorithm.

Go back