Fast Text Matching with Prefix Trees
A prefix tree is a data structure designed for efficient text operations. It provides us with the ability to perform fast search, add, and pattern matching operations in large text collections.
Prefix trees are the unsung heroes behind many technologies we use daily, from auto-complete functions in text editors to complex DNA sequence analysis in bioinformatics.
How Prefix Trees Work
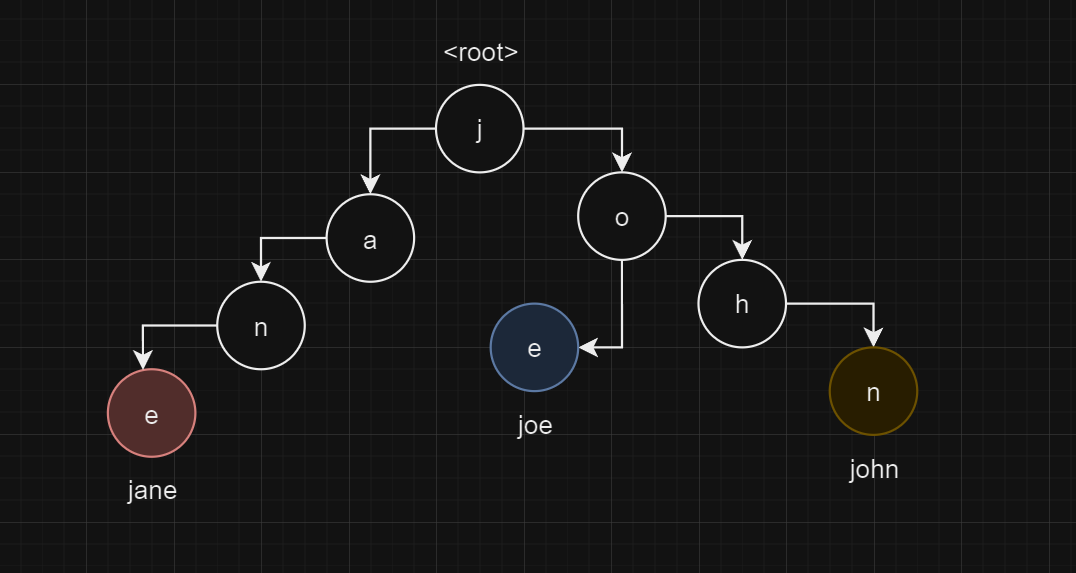
A prefix tree consists of nodes. Each node represents a symbol. For example, we can create a prefix tree from the word “hello” like this:
h-e-l-l-o
One of the main advantages of prefix trees is their ability to store sets of strings with common prefixes efficiently. For example, if we have the strings “maşın”, “maşınçı”, and “maşınqayırma”, they will share a common path for “maşın” and then branch out.
m-a-ş-ı-n*-q-a-y-ı-r-m-a*
|
c - ı*
When we search for a string, we start from the root and iterate over the symbols in the search string. If the current symbol exists in the tree, we move to the next symbol. If all symbols are found, then the string is considered to be in the prefix tree’s set. Considering that we only iterate as many times as there are symbols in the search string, this is a very efficient search. Therefore, the time complexity is O(m), where m is the length of the search string. We will discuss this in more detail later.
Example 1
Search word "maşın":
Tree:
m-a-ş-ı-n*-q-a-y-ı-r-m-a*
|
c - ı*
Steps:
1. "m" - exists, next "a"
2. "a" - exists, next "ş"
3. "ş" - exists, next "ı"
4. "ı" - exists, next "n"
5. "n" - exists, next "q" or "c"
6. Word exists in the set: because there is a flag at the "n" node.
No need to continue.
Example 2
Search word "maşa":
Tree:
m-a-ş-ı-n*-q-a-y-ı-r-m-a*
|
c - ı*
Steps:
1. "m" - exists, next "a"
2. "a" - exists, next "ş"
3. "ş" - exists, next "ı"
4. Word does not exist in the set: because the next symbol is not "a".
Example 3
Search word "maşınqayırma":
Tree:
m-a-ş-ı-n*-q-a-y-ı-r-m-a*
|
c - ı*
Steps:
1. "m" - exists, next "a"
2. "a" - exists, next "ş"
3. "ş" - exists, next "ı"
4. "ı" - exists, next "n"
5. "n" - exists, next "q" or "c"
6. "q" - exists, next "a"
7. "a" - exists, next "y"
8. "y" - exists, next "ı"
9. "ı" - exists, next "r"
10. "r" - exists, next "m"
11. "m" - exists, next "a"
12. "a" - exists
13. Word exists in the set: there is a flag at the "a" node.
Writing the Code
Now we’ve reached the most interesting part! Let’s write the code. It can be written in any programming language, but let’s do it in TypeScript. Our code will be very simple, consisting of two classes, then we will add words and perform searches to see the results. Read the first code and try to understand the logic; if you have trouble, there is a more detailed explanation below.
// Node class
class SuffixTreeNode {
constructor(
public nextNodes = {},
public isEndOfWord = false
) {}
}
// Prefix Tree class
class SuffixTree {
private rootNode: SuffixTreeNode;
constructor() {
this.rootNode = new SuffixTreeNode();
}
public addWord(word: string): void {
let currentNode = this.rootNode;
for (const symbol of word) {
if (!currentNode.nextNodes[symbol]) {
currentNode.nextNodes[symbol] = new SuffixTreeNode();
}
currentNode = currentNode.nextNodes[symbol];
}
currentNode.isEndOfWord = true;
}
public searchWord(word: string): boolean {
let currentNode = this.rootNode;
for (const symbol of word) {
if (!currentNode.nextNodes[symbol]) {
return false;
}
currentNode = currentNode.nextNodes[symbol];
}
return currentNode.isEndOfWord;
}
}
// Create an object from the SuffixTree class
const tree = new SuffixTree();
// Add words to the tree
tree.addWord("maşın");
tree.addWord("maşınqayırma");
tree.addWord("maşa");
// Search for words
console.log(tree.searchWord("maşın")); // true
console.log(tree.searchWord("maşa")); // true
console.log(tree.searchWord("maşınqayırma")); // true
console.log(tree.searchWord("maaş")); // false
console.log(tree.searchWord("maşınka")); // false
Creating the Prefix Tree
Creating the prefix tree starts with defining the root node. This node is the starting point of the tree, and other subsequent nodes are considered its children. The Node class represents a node in the tree and contains the properties nextNodes (child nodes) and isEndOfWord (a flag indicating whether the node is the end of a word). The SuffixTree class represents the prefix tree and contains the private property rootNode (the root node).
Adding Words
The process of adding words to the tree is handled by the addWord method. This method traverses the tree for each symbol in the word. If a symbol does not have a corresponding child node, a new node is created. When the end of the word is reached, the isEndOfWord property of the last node is set to true.
Searching for Words
The process of searching for words in the tree is handled by the searchWord method. This method traverses the tree for each symbol in the word. If a symbol does not have a corresponding child node, the method returns false. If all symbols are traversed and the isEndOfWord property of the last node is set to true, the method returns true.
You can play with the code here.
Time Complexity
One of the most notable features of prefix trees is the time complexity of operations performed on them. After the tree is built, searching for a string of length m takes O(m) time in the worst case. Adding a new string is also efficient. Adding a new string of length m will only take O(m) time. Building the tree for a dataset of total length n can take O(n) time, or O(n^2) in the worst case.
Benchmark Results
To demonstrate the efficiency of prefix trees, let’s look at some benchmark results. Here, we compare the prefix tree method with a simple iterative method.
| Method | Initialization Time | Average Search Time per Loop | Total Time for 40 Loops |
|---|---|---|---|
| Prefix Tree | 601 ms | 4.5 ms | 180 ms |
| Iterative Method | 0 ms | 1335.5 ms | 53420 ms |
These benchmarks were performed on a dataset of 1 million English words, with 1000 random words searched.
Although the memory usage of a prefix tree is relatively high, it can be used in modern systems, especially considering the performance advantages it provides.